一：队列基本概念

（1）队列的定义

队列(Queue)：是一种只允许在一端插入，在另一端删除的线性表。我们把允许插入的一端称之为队尾(rear)，把允许删除的一端称之为队头(front)。不含任何数据元素的队列称之为空队列。队列遵循先进先出(FIFO)原则

生活中的排队就是典型的队列
有时我们使用电脑时，会突然感觉电脑卡住了，乱点鼠标、乱按键盘也没有什么效果，然后突然它就像清醒了一般，把你刚才的所有操作全部执行了一遍。其实这是因为操作系统中的多个程序需要通过一个通道输出，而按先后次序排队等待造成的

（2）入队和出队

入队：是队列的插入操作

出队：是队列的删除操作

如下

入队顺序： $a_{1}$ -> $a_{2}$ -> $a_{3}$ -> $a_{4}$ -> $a_{5}$
出队顺序： $a_{1}$ -> $a_{2}$ -> $a_{3}$ -> $a_{4}$ -> $a_{5}$

（3）队列的操作

一个队列的基本操作如下

InitQueue(&Q)：初始化队列
DestoryQueue(&Q)：销毁队列
EnQueue(&Q,x)：入队
DeQueue(&Q,&x)：出队
GetHead(Q,&x)：读队头元素
QueueEmpty(Q)：队列判空

二：Queue使用

Queue：数据接口中的队列对应于Java集合框架中的Queue，注意它是一个接口，底层由链表实现，所以在实例化时必须实例化为LinkedList对象

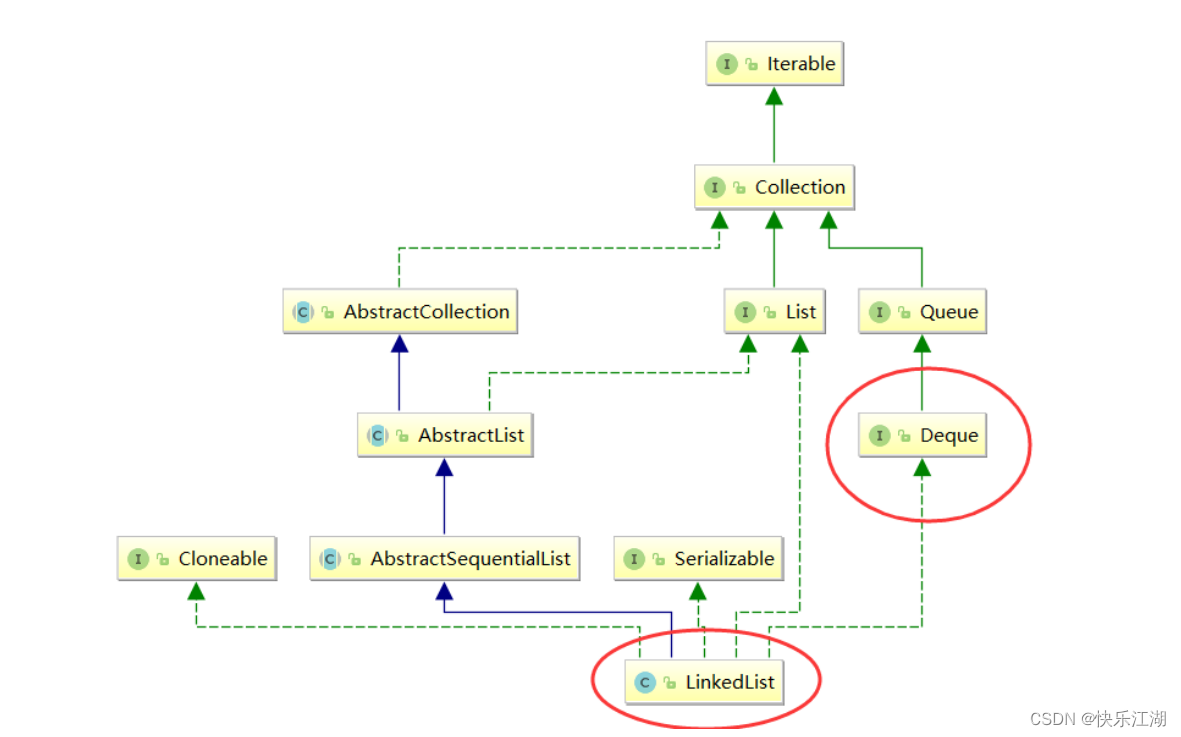
涉及方法如下

boolean offer(E, e)：入队列
E poll()：出队列
peek()：获取队头元素
int size()：获取队列中有效元素个数
boolean isEmpty()：判断队列是否为空

下面是一个例子

public class TestDemo {
    public static void main(String[] args) {
        Queue<Integer> q = new LinkedList<>();
        q.offer(12);
        q.offer(34);
        q.offer(56);
        q.offer(78);
        q.offer(90);

        System.out.println("获取队头元素：" + q.peek());
        q.poll();
        System.out.println("出队2个元素再获取队尾元素：" + q.peek());
        System.out.println("判断队列是否为空：" + q.isEmpty());
    }
}

三：队列模拟实现

（1）链式队

A：链式队列的定义

链式队列：其本质仍然是单链表，不过只能尾进头出。为了操作方便，将front指针指向头结点,将rear指针指向队尾结点

于是，在队列为空时，front和rear都将指向头结点

因此链式队列结构定义如下

typedef struct QNode//结点
{
	DateType data;
	struct QNode* next;
}QNode;

typedef struct LinkQueue//链式栈
{
	QNode* rear;//队尾指针
	QNode& front;//队头指针
}LinkQueue;

B：入队

入队时，在链表尾部插入结点

bool EnQueue(LinkQueue& Q,DataType e)
{
	QNode* NewNode=(QNode*)malloc(sizeof(QNode));
	if(NewNode==NULL)
		return false;
	NewNode->data=e;
	NewNode->next=NULL;
	Q->rear->next=NewNode;
	Q->rear=NewNode;//新节点作为队尾结点
}

C：出队

删除时相当于链表的头删

bool DeQueue(LinkQueue& Q,DataType& e)
{
	Node* p;//用于释放
	if(Q.front==Q.rear)
		return false;
	p=Q.front->next;
	*e=p->data;
	Q.front->next=p->next;
	
	if(p==Q.rear)//注意如果队头就是队尾，那么删除是空队列
		Q.rear=Q.frontl
	free(p);
	return true;
}

D：代码

队列的实现也有顺序结构和链式结构两种，这里以链式结构为例

package myQueue;

public class MyQueue {
    //结点定义
    static class Node{
        public int val;
        public Node next;
        public Node(int val){
            this.val = val;
        }
    }

    //队列头结点和尾节点
    public Node front;
    public Node rear;

    //入队
    public void offer(int val){
        Node node = new Node(val);
        if(this.front == null){
            this.front = node;
            this.rear = node;
        }else{
            this.rear.next = node;
            this.rear = node;
        }
    }

    //出队
    public int poll(){
        if(this.front == null){
            return -1;
        }
        int retVal = this.front.val;
        if(this.front.next == null){
            this.front = this.rear =null;
        }else {
            this.front = this.front.next;
        }
        return retVal;
    }

    //查看队头元素
    public int peek(){
        if(this.front == null){
            return -1;
        }
        return this.front.val;
    }
}

（2）顺序队（循环队列）

使用数组来完成栈的顺序存储结构是没有什么太大问题的（除了容量），但是如果用数组来实现队列的顺序存储结构却会产生很大问题

A：单纯的顺序存储的不足之处及font指针和rear指针

1：队列采用顺序存储结构，如何解决出队列时元素移动导致时间复杂度很大的问题？

假设一个队列有 $n$ 个元素，则顺序存储的队列需要建立一个大于 $n$ 的数组，并把队列的所有元素存储在数组的前 $n$ 个单元。数组下标为0的一端就是队头，如下

那么入队列实际就是在队尾追加一个元素，不需要移动任何元素，这一点没什么问题

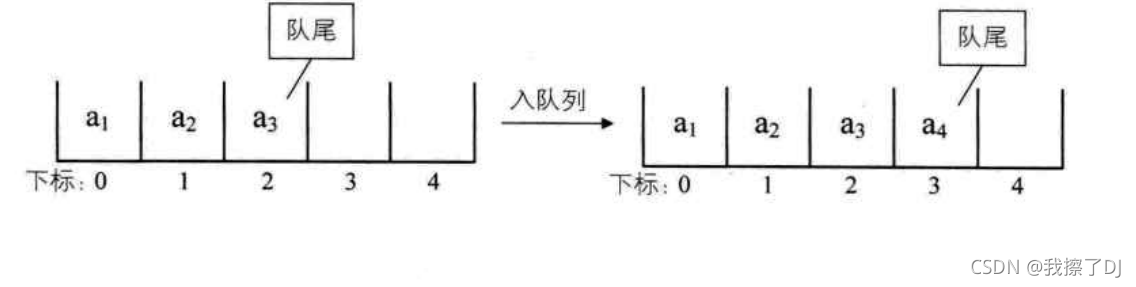
但是要命的地方在于出队列，因为它限制在了队头也即下标为0的地方进行删除，那么这意味着队头元素移出之后，剩余元素必须向前移动，以保证有元素始终处于队头位置，这样的话时间复杂度将达到 $O(n)$

因此对于这一点解决方法是：引入front指针指向队头元素，rear指针指向队尾元素的下一个位置

rear必须要指向队尾元素的下一个位置，否则无法区分队满还是队空（当rear=front就是队空了）

所以大家可以看到，在空队列时有rear=front=0。然后 $a_{1}$ 、 $a_{2}$ 、 $a_{3}$ 、 $a_{4}$ 依次入队。此时front指针不动，而rear指针指向了队尾元素的下一个位置

接着出队 $a_{1}$ 、 $a_{2}$ ，于是front指针指向下标为2的位置，而rear不变

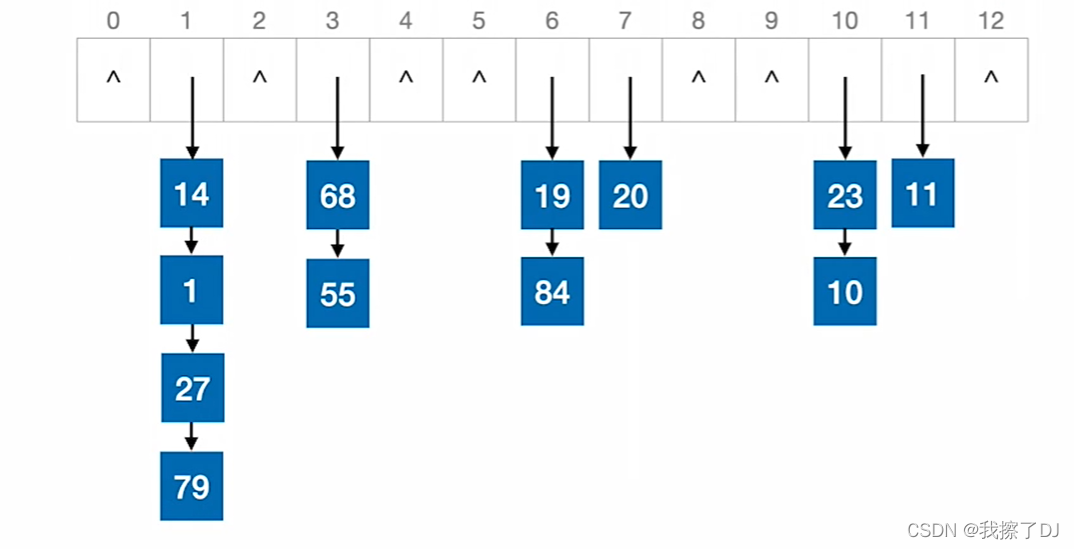
2：出队、入队都有可能导致数组越界，如何解决？

紧接着上面那种情况，rear已经指向了4，如果再入队一个元素 $a_{5}$ ，那么rear岂不是越界了？

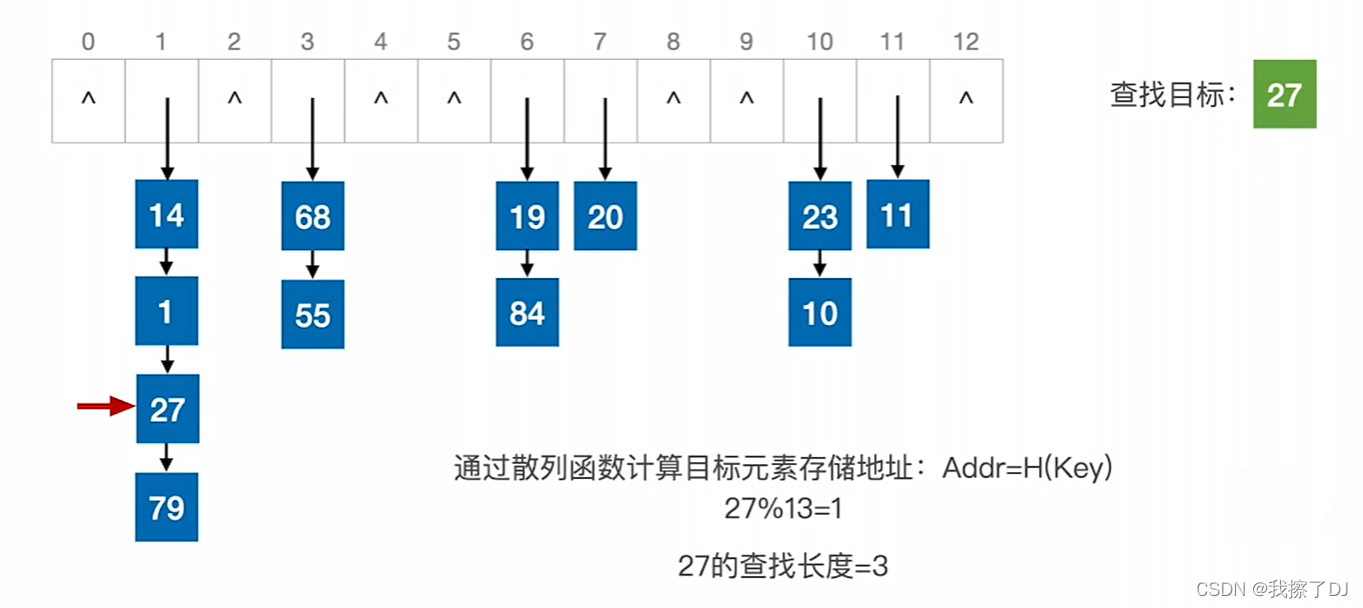
如果反映在数组上，我们知道编译器一定会给我们反馈“越界”的信息，但是很明显上面还有空余位置，所以这是一种假溢出

因此如果要完美的实现队列的顺序存储结构就必须要做一定的改进——循环队列

B：循环队列概念及队空队满条件

循环队列：为了解决假溢出问题，可以将数组“头尾相接”形成一种逻辑上的环形结构

这种“环形”只是一种逻辑上的感觉，其底层仍然是连续的空间，想要实现操作上的环形那么就必须要对其下标的变换做一定的文章（具体为什么是下面这样我就不细说了，其实就是利用了%元素，例如1%12会把结果映射到0~11这个范围）

rear移动时：rear=(rear+1)%Maxsize)
front移动时：front=(front+1)%Maxsize)

所以使用这种方式，当 $a_{5}$ 插入时，rear=(4+1)%5=0，于是就又回到了开头

数组空间毕竟是有限的，那么这样的结构其队空队满的条件是什么呢？如下

队空：rear=front
队满：front=(rear+1)%Maxsize

比如下面，rear开始为1，插入 $a_{7}$ 后,rear=(1+1)%5=3=front，此时队满

另外还有一种问题就是求队列长度，其通用的公式为:（rear-front+Maxsize）%Maxsize

C：循环队列定义

循环队列结构定义如下

typedef struct
{
	DataType data[MaxSize];
	int front;//头指针
	int rear;//尾指针。若队列不空，指向队尾元素的下一个位置
}SqQueue;

初始化代码如下

bool InitQueue(SqQueue& Q)
{
	Q.front=0;
	Q.rear=0;
	return true;
}

D：入队

入队：入队时，先元素赋值，后rear指针+1（因为要保证rear指向队尾下一个位置）

bool EnQueue(SqQueue& Q,DataType e)
{
	if(Q.front==(Q.rear+1)%MaxSize)
		return false;//队满
	Q.data[Q.rear]=e;
	Q.rear=(Q.rear+1)%MaxSize;
	
	return true;
}

E：出队

出队：出队时，直接front+1即可（front要始终指向队头元素）

bool DeQueue(SqQueue& Q,DataType& e)
{
	if(Q.front==Q.rear)
		return false;//队空
	*e=Q.data[Q.front];
	Q.front=(Q.front+1)%MaxSize;
	return true;
}

F：代码

package myCircularQueue;

public class MyCircularQueue {
    public int[] elem;
    public int usedSize;
    public int front;//队头
    public int rear;//队尾

    public MyCircularQueue(int k){
        this.elem = new int[k];
    }

    //入队
    public boolean enQueue(int value){
        if(this.isFull()){
            return false;
        }
        this.elem[rear] = value;
        this.rear = (this.rear+1) % (this.elem.length);
        return true;
    }

    //出队
    public boolean deQueue(){
        if(this.isEmpty()){
            return false;
        }
        this.front = (this.front+1)%(this.elem.length);
        return true;
    }

    //获取队头元素
    public int getFront(){
        if(isEmpty()) {
            return -1;
        }
        return this.elem[this.front];
    }

    //获取队尾元素
    public int getRear(){
        if(isEmpty()) {
            return -1;
        }
        int index = this.rear-1;
        if(this.rear == 0) {
           index = this.elem.length - 1;
        }
        return this.elem[index];
    }

    //判空
    public boolean isEmpty(){
        return this.rear == this.front;
    }
    //判满
    public boolean isFull(){
        return (this.rear+1)%(this.elem.length) == this.front;
    }
}

目录CONTENT

第十四章第三节2：Java集合框架之队列Queue