一：树基本概念

（1）树的定义

树(Tree)：这是一种非线性结构。是 $n$ ( $n\geq 0$ )个有限结点组成的一个具有层次关系的集合，与现实生活中的树十分相像，只不过它是倒挂的。 $n$ =0时称这样的树为空树

树结构特点：在任何一个非空树中

有且只有一个特定的称为根(Root)的结点
当 $n$ >1时，其余结点可以分为 $m$ ( $m$ >0)个互不相交的有限集合 $T_{1}$ 、 $T_{2}$ … $T_{m}$ ,其中每一个集合本身又是一颗树，并且称为根的子树(Sub Tree)。因此树是具有递归性质的

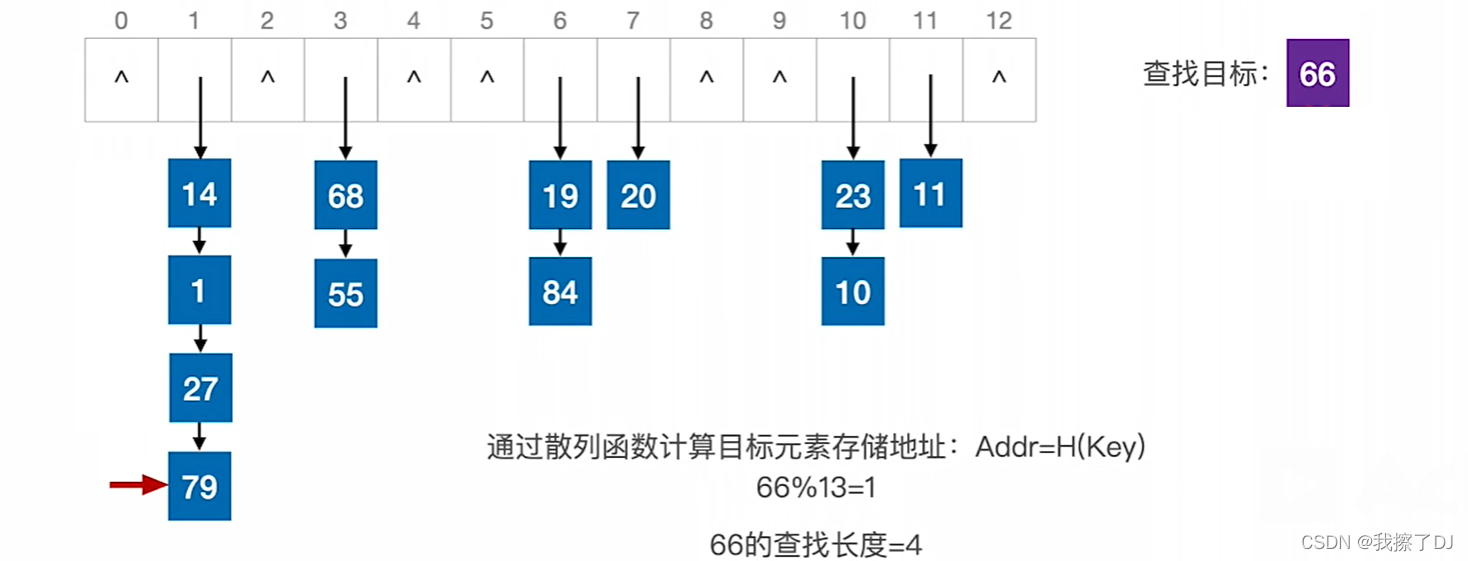
$T_{1}$ 和 $T_{2}$ 是根节点 $A$ 的子树

（2）结点分类

树结点结构：包含一个数据元素和指向其子树的分支

结点分类：除根节点外，其余结点有且只有一个结点

根节点：只有后继没有前驱，对于非空树，有且只有一个
叶子结点（终端结点）：没有后继结点的结点（度为0）
分支结点（非终端结点）：有后继结点的结点（度为0），除根节点外分支结点也称为内部结点

（3）结点关系（相关术语）

下面的这些概念，了解即可，不用刻意记忆

术语	描述	举例
结点	A，B，C等都是结点，结点不仅包含数据元素，而且包含指向子树的分支。	A结点不仅包含元素A，而且包含三个指向子树的指针
结点的度	结点拥有的子树或分支个数	A结点有三颗子树，A的度为3
树的度	树中各结点度的最大值	A,D结点的度最大为3，故树的度为3
叶子结点	度为0的结点	F,G,I,J,K,L,M均为叶子结点
非叶结点	度不为0的结点	A,B,C,D,E,H,均为非叶结点
孩子	某结点子树的根	A结点的孩子为B,C,D
双亲	与孩子的定义对应	B,C,D的双亲都是A
兄弟	同一个双亲的孩子互为兄弟	B,C,D互为兄弟
祖先	从根到某结点的路径上所有的结点，都是该结点的祖先	K的祖先是A,B,E
子孙	以某结点为根的子树中的所有结点	D的子孙是H,I,J,M
层次	根节点为第一层，根的孩子是第二层次，以此类推	结点F处在第三层
结点的深度	是指从根节点到该结点路径上的结点个数	\|
结点的高度	从某结点往下走可能到达多个叶子结点，对应了通往这些叶子结点的路径，其中最长的那条路径上的结点的个数称其为结点的高度	D的高度为3
树的高度(深度)	树中结点的最大层次	根节点的高度就是树的高度
堂兄弟	双亲在同一层的结点互为堂兄弟	G和H互为堂兄弟
有序树	树中结点的子树从左至右是有次序的，不能交换	\|
无序树	树中结点的子树没有顺序，可以任意交换	\|
丰满树	除了最底层外，其他层都是满的	\|
森林	若干互不相交的树的集合	上面的树，将根结点A去除，剩余的就一个森林
有序树	树中结点从左至右是有次序的，不能交换	\|
无序树	树中结点从左至右是无次序的，可以交换	\|

注意结点的层次（深度）默认从1开始

（4）常用性质

性质1：结点数=总度数+1

结点数为13，度数为12

性质2：度为 $m$ 的树和 $m$ 叉树区别

度为 $m$ 的树	$m$ 叉树
任意结点的度小于等于 $m$ ，也即最多 $m$ 个孩子	任意结点的度小于等于 $m$ ，也即最多 $m$ 个孩子
至少有一个结点度为 $m$	允许所有结点的度都小于 $m$
一定是非空树，至少有 $m+1$ 个结点	可以是空树

性质3：度为 $m$ 的树第 $i$ 层至多有 $m^{i-1}$ 个结点，其中 $i$ 大于等于1

性质4：高度为 $h$ 的 $m$ 叉树至少有 $h$ 个结点；高度为 $h$ 度为 $m$ 的树至少有 $h$ + $m$ -1个结点

性质5：具有 $n$ 个结点的 $m$ 叉树的最小高度为 $\lceil log_{m}(n(m-1)+1)\rceil$

二：二叉树基本概念

（1）二叉树定义

二叉树(Binary Tree)：是 $n$ 个( $n$ $\geq 0$ )结点的有限集合，其中每个结点最多有两颗子树，也即二叉树度最大为2，同时二叉树子树有次序之分，不能颠倒。结点数为0的二叉树称之为空二叉树

（2）二叉树五种形态

我们所见到的二叉树无外乎以下五种

空二叉树
只有左子树
只有右子树
只有根节点
左右子树都存在

（3）特殊的二叉树

满二叉树：满二叉树它的每一层的结点数都达到了最大值。如果一个满二叉树有 $h$ 层，那么结点总数为2 $^{h}$ -1个

只有最后一层是叶子结点
不存在度为1的结点
若按层序从1开始编号，结点 $i$ 的左孩子的编号就为 $2i$ ，结点 $i$ 的右孩子的编号就为 $2i+1$ ，同时其父节点为 $\lfloor \frac{i}{2} \rfloor$

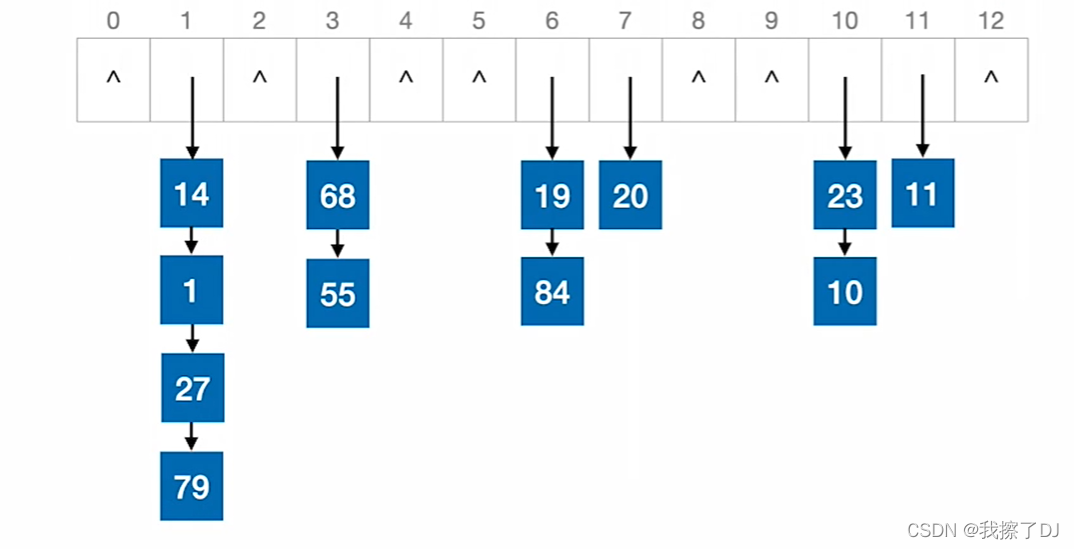
完全二叉树：一个完全二叉树是由对应的满二叉树进行删除而来的，删除的时候必须从右向左，从下到上，不能跳着删除

只有最后两层可能有叶子结点
最多只有一个度为1的结点
如果某个结点只有一个孩子，那么它一定是左孩子
若按层序从1开始编号，结点 $i$ 的左孩子的编号就为 $2i$ ，结点 $i$ 的右孩子的编号就为 $2i+1$ ，同时其父节点为 $\lfloor \frac{i}{2} \rfloor$
若按层序从1开始编号,当 $i \leq \lfloor \frac{n}{2} \rfloor$ 时该结点为分支结点，当 $i > \lfloor \frac{n}{2} \rfloor$ 时该结点为叶子结点

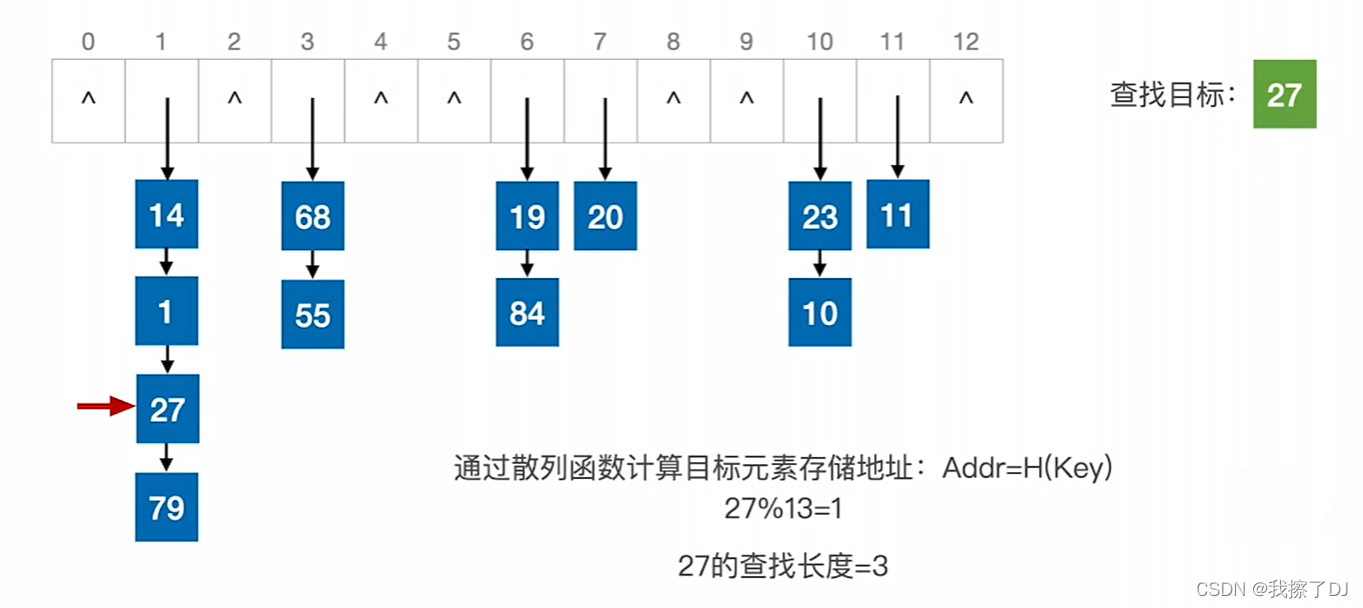
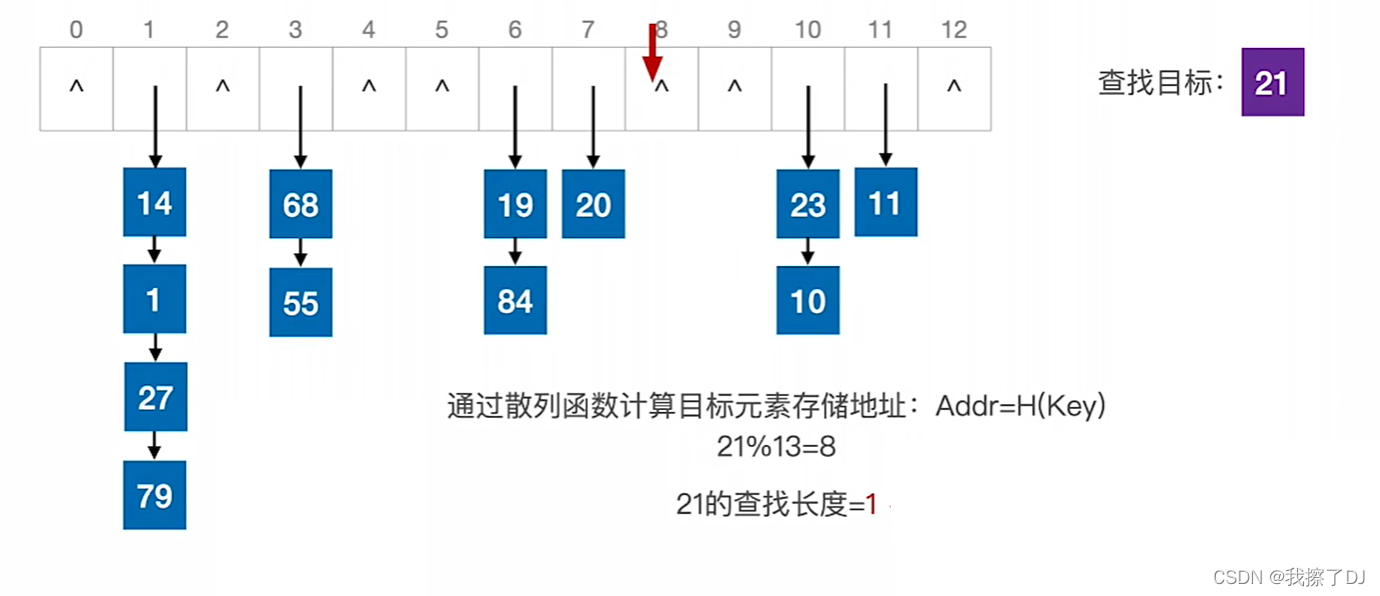
二叉排序树：一颗二叉树若具有以下性质，则称为二叉排序树

左子树上所有结点的关键字值均小于根结点的关键字
右子树上所有结点的关键字值均大于根结点的关键字
左子树和右子树又各是一颗二叉排序树

平衡二叉树：树上任一结点的左子树和右子树的高度之差不超过1

（4）二叉树常考性质

性质1：非空二叉树中，叶子结点（度为0的结点）总比度为2的结点多1个

首先需要明白，度为0的结点，引出0个分支；度为1的结点引出1个分支，度为2的结点引出2个分支，依次类推
假设一个二叉树中叶子结点有n₀个，那么它引出0×n₀条分支，单分支结点数为n₁个，它就会引出1×n₁条分支，双分支结点数为n₂，它引出2×n₂条分支。于是总的结点数为n₀+n₁+n₂，总分支数为n1+2×n₂条
任何一个树，总分支（度数）数=总结点数-1，于是由②可知n1+2×n₂=n₀+n₁+n₂-1，化简得到n₀=n₂+1.

这条性质要注意灵活应用，很多时候不会这样直接考。比如某道题问“二叉树的总的结点数为n，空指针多少？” 我们可以把所有的空指针都看作叶子结点，也就是说这个二叉树所有节点都是双分支结点，根据叶子结点数=双分支结点数+1，所以在本树中，叶子结点数（空指针数）=双分支结点数（总的结点数）+1，也就是n+1.

性质2：二叉树第 $i$ 层至多有 $2^{i-1}$ 个结点

性质3：高度为 $h$ 的二叉树至多有 $2^{h}-1$ 个结点（也就是满二叉树）

性质4：具有 $n$ 个结点的完全二叉树的高度为
$h=\left \lfloor log_{2}n\right \rfloor+1或\left \lceil log_{2}(n+1)\right \rceil$

性质5：对于完全二叉树，可以由结点数 $n$ 推出度为0、1和2的结点个数为 $n_{0}$ 、 $n_{1}$ 和 $n_{2}$ 。因为完全二叉树做多只有一个度为1的结点，即 $n_{1}$ =0或 $n_{1}$ =1，又因为 $n_{0}$ = $n_{2}$ +1，故 $n_{0}$ + $n_{2}$ =2 $n_{2}$ +1一定为奇数，所以

若完全二叉树有 $2k$ (偶数)个结点，则必有 $n_{1}=1$ 、 $n_{0}=k$ 、 $n_{2}=k-1$
若完全二叉树有 $2k-1$ (奇数)个结点，则必有 $n_{1}=0$ 、 $n_{0}=k$ 、 $n_{2}=k-1$

（5）二叉树存储结构——二叉链表

二叉链表：二叉树每个结点最多有两个孩子，所以为其设置一个数据域和两个指针域，称这样的链表为二叉链表

如下，其中data为数据域，lchild和rchild都是指针域，分别指向该结点的左孩子和右孩子

其结点结构定义如下

typedef struct BTNode
{
	DataType data;
	struct BTNode* lchild;
	struct BTNode* rchild;
}BTNode;

三：二叉树的遍历

（1）深度优先遍历

A：先序遍历-根左右(NLR)

先序遍历：第一次遇到这个结点访问，第二次遇到或第三次遇到时跳过该结点直接访问下一个结点

也即若二叉树为空，则返回空，否则先访问根节点，然后先序遍历左子树，再先序遍历右子树

先序遍历算法：二叉树定义采用的递归形式，所以其遍历代码也可以采用递归，形式极其简单

void PreOrderTraverse(BTNode* root)
{
	if(root==NULL)
		return NULL;
	printf("%c",root->data);//结点访问操作，也可以是其他
	PreOrderTraverse(BTNode->lchild);//再先序遍历左子树
	PreOrderTraverse(BTNode->rchild);//最后先序遍历右子树
	
}

B：中序遍历-左根右(LNR)

中序遍历：第一次遇到结点跳过，第二次再遇到结点访问，第三次遇到跳过

也即若树为空，则返回空，否则从根节点开始（注意并不是先访问根节点），中序遍历根节点的左子树，然后是访问根节点，最后中序遍历右子树

中序遍历算法：二叉树定义采用的递归形式，所以其遍历代码也可以采用递归，形式极其简单

void InOrderTraverse(BTNode* root)
{
	if(root==NULL)
		return NULL;
	InOrderTraverse(BTNode->lchild);//中序遍历左子树
	printf("%c",root->data);//结点访问操作，也可以是其他
	InOrderTraverse(BTNode->rchild);//中序遍历右子树
	
}

C：后序遍历-左右根(LRN)

后序遍历：前两次遇见结点不访问，最后一次遇见时访问

也即若树为空，则返回空。否则从左到右先叶子后结点的方式遍历访问左右子树，最后根节点

后序遍历算法：二叉树定义采用的递归形式，所以其遍历代码也可以采用递归，形式极其简单

void PostnOrderTraverse(BTNode* root)
{
	if(root==NULL)
		return NULL;
	PostOrderTraverse(BTNode->lchild);//后序遍历左子树
	PostOrderTraverse(BTNode->rchild);//后序遍历右子树
	printf("%c",root->data);//结点访问操作，也可以是其他
	
}

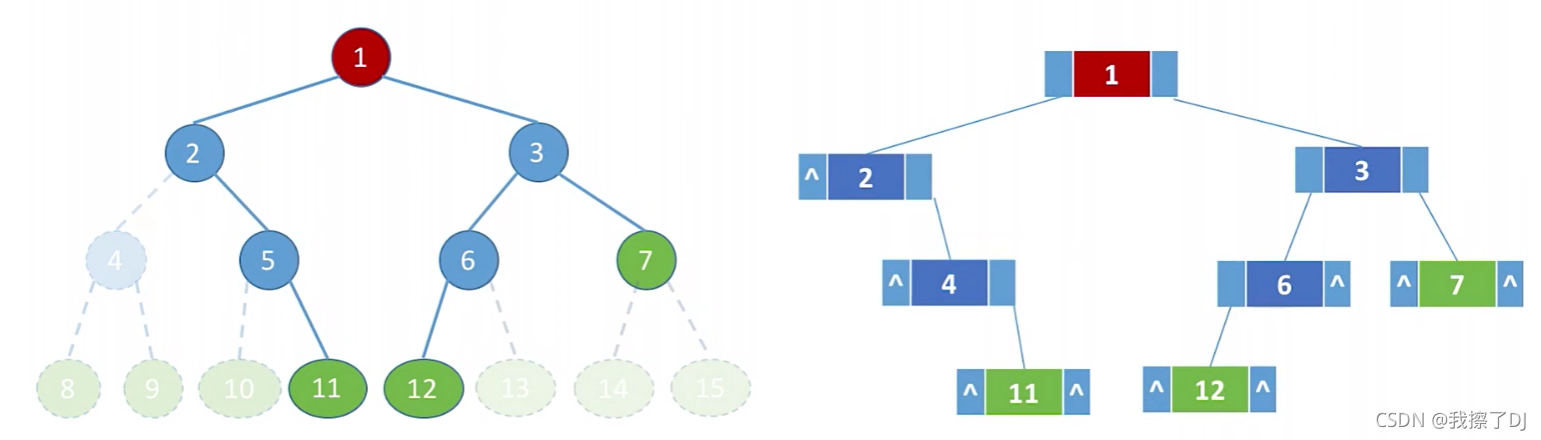
（2）层次遍历

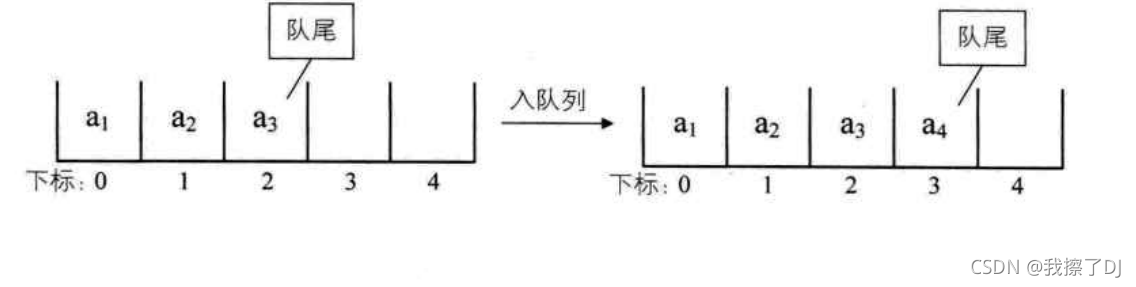
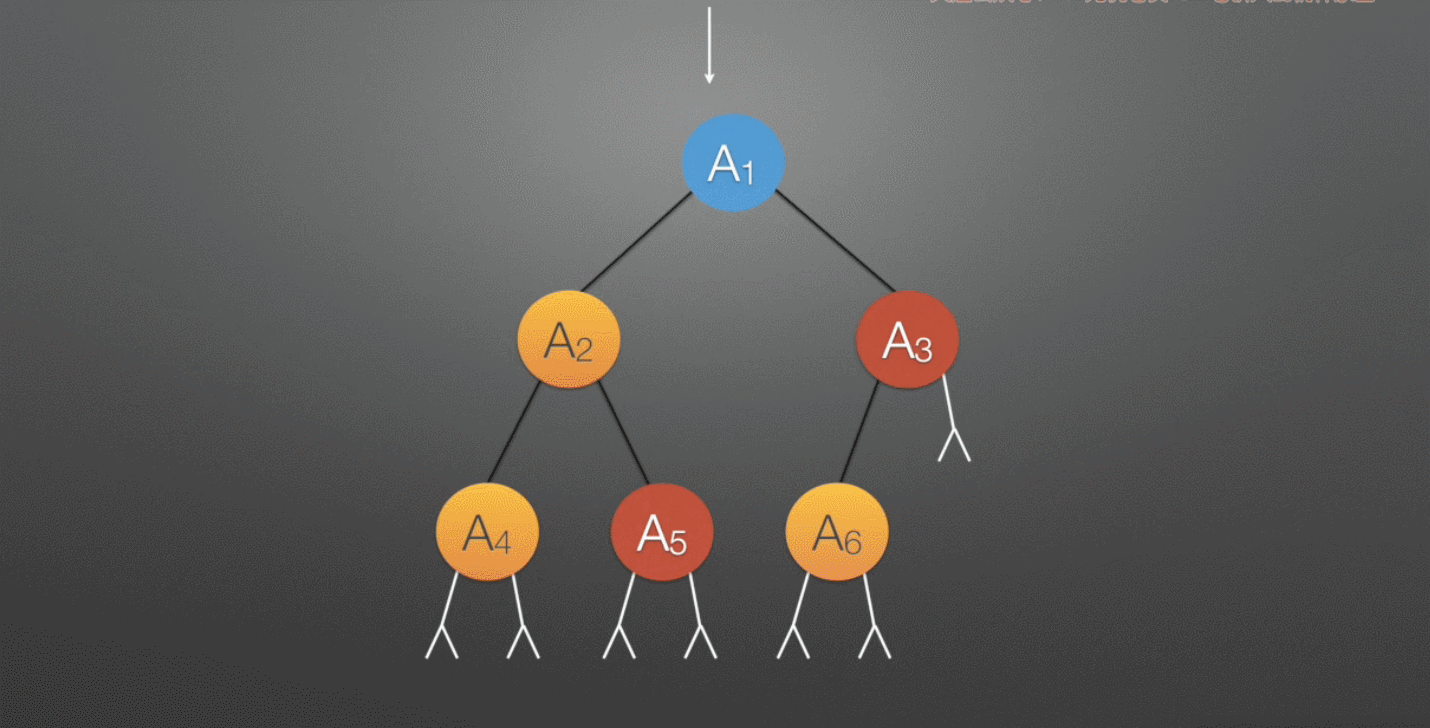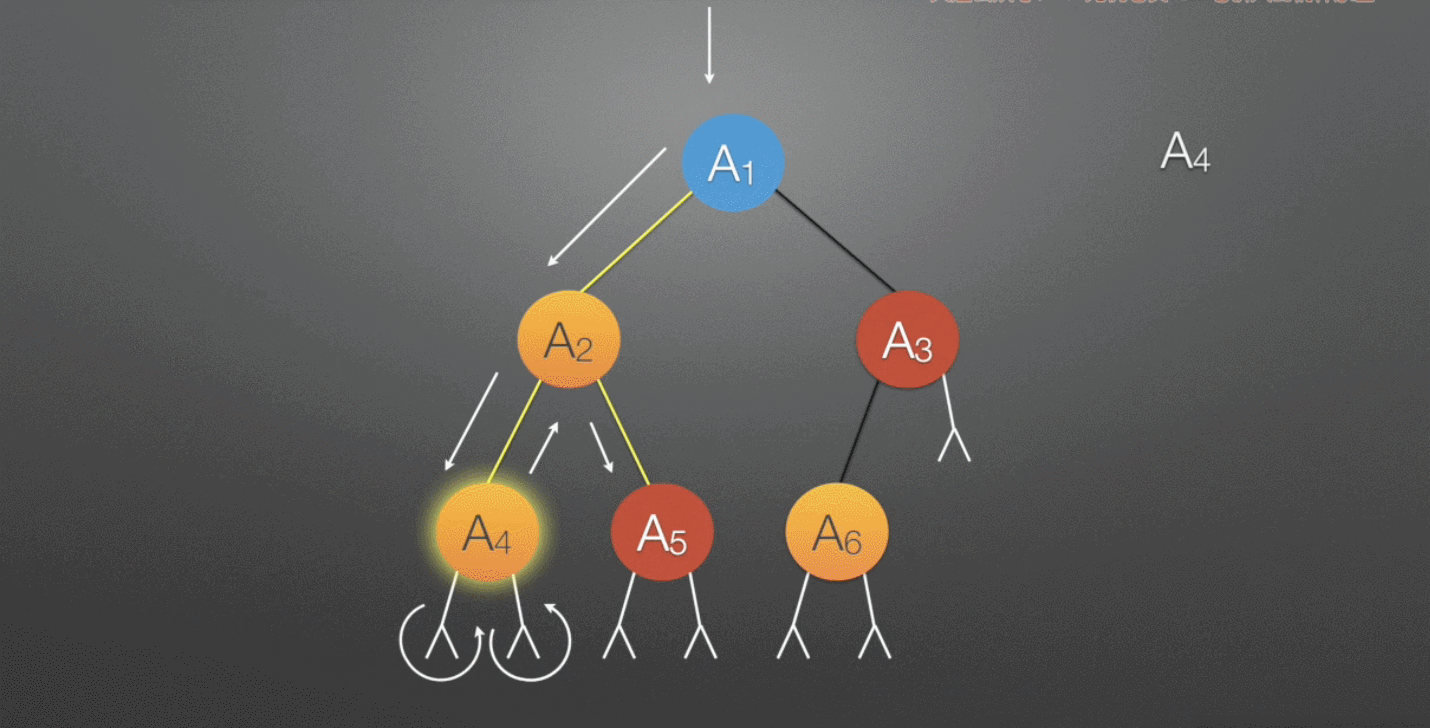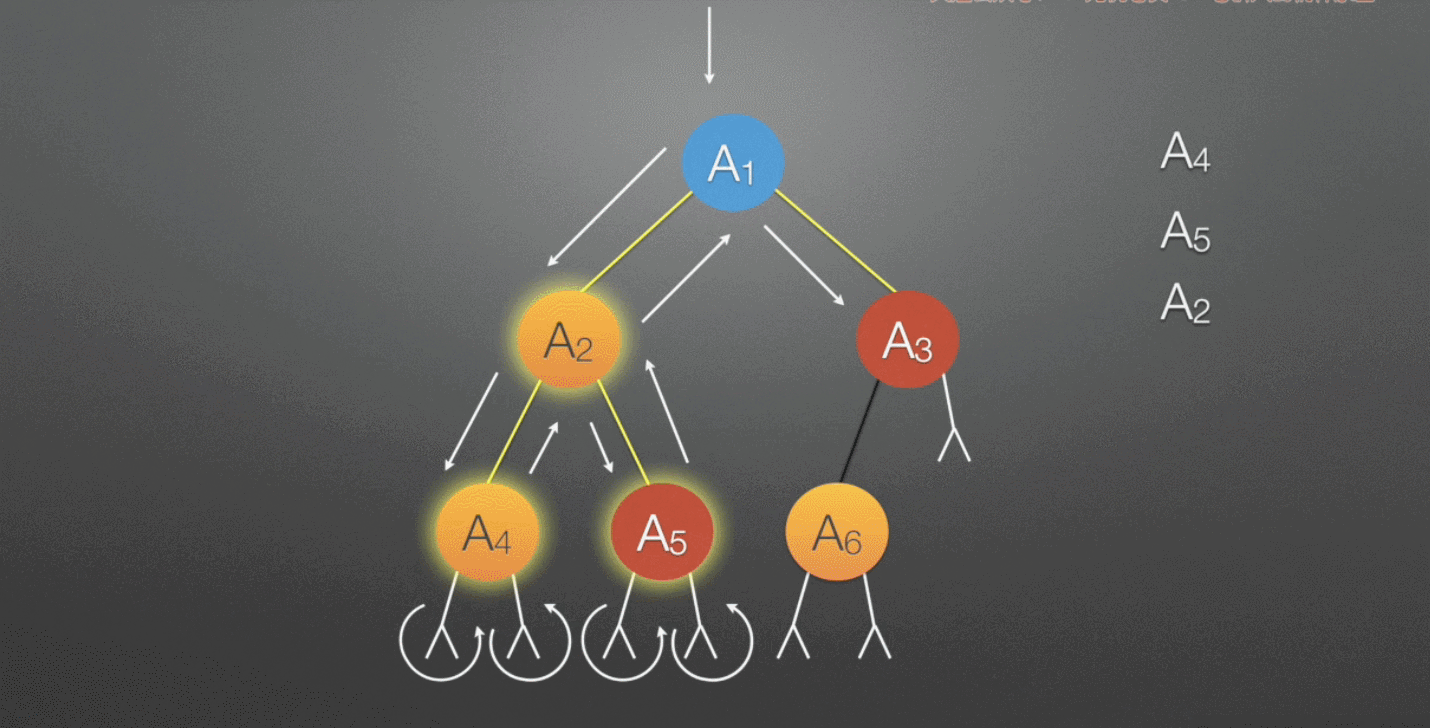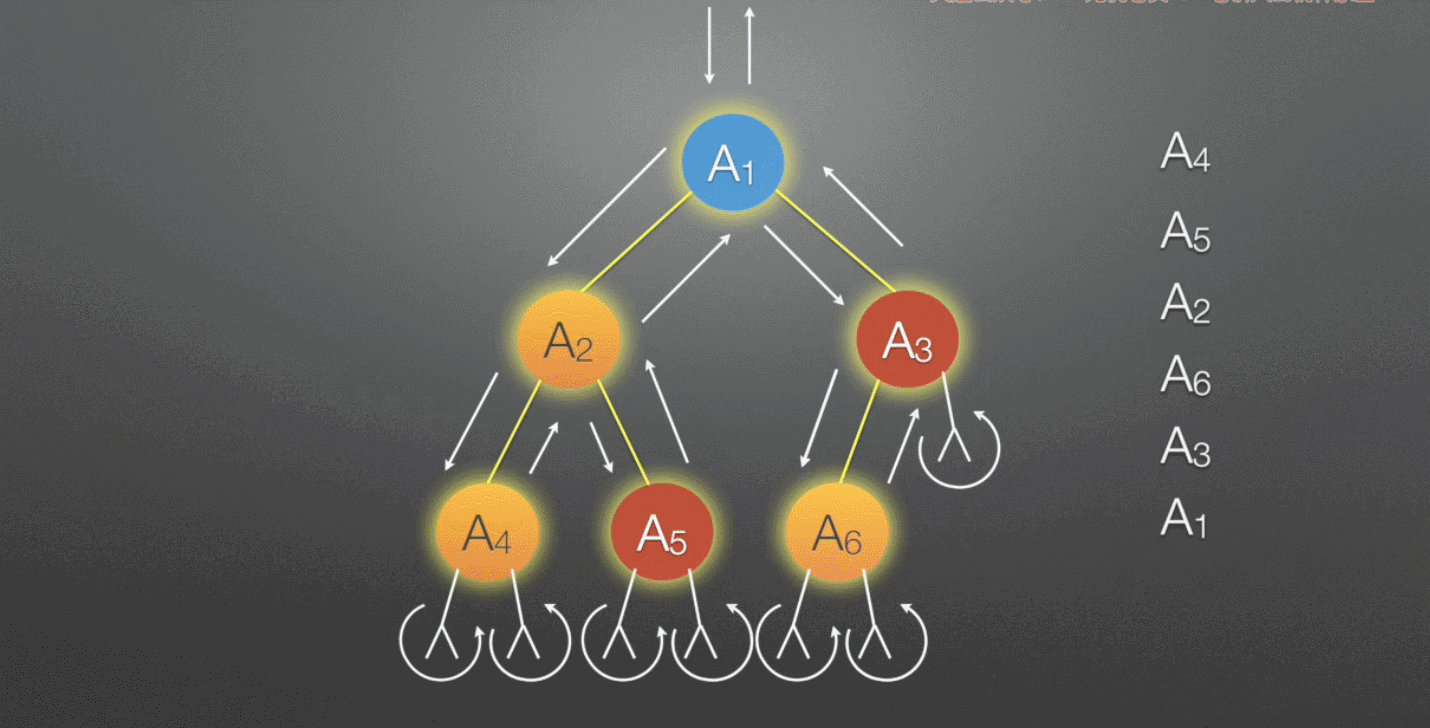
层次遍历：需要借助队列完成。若树为空，则返回空，然后从上至下，从左至右依次访问结点

初始化一个辅助队列
根结点入队
若队列非空，则队头结点出队，访问该结点，然后将其左、右孩子（如果有）插入队尾
重复第三步，直至队列为空

具体过程如下图

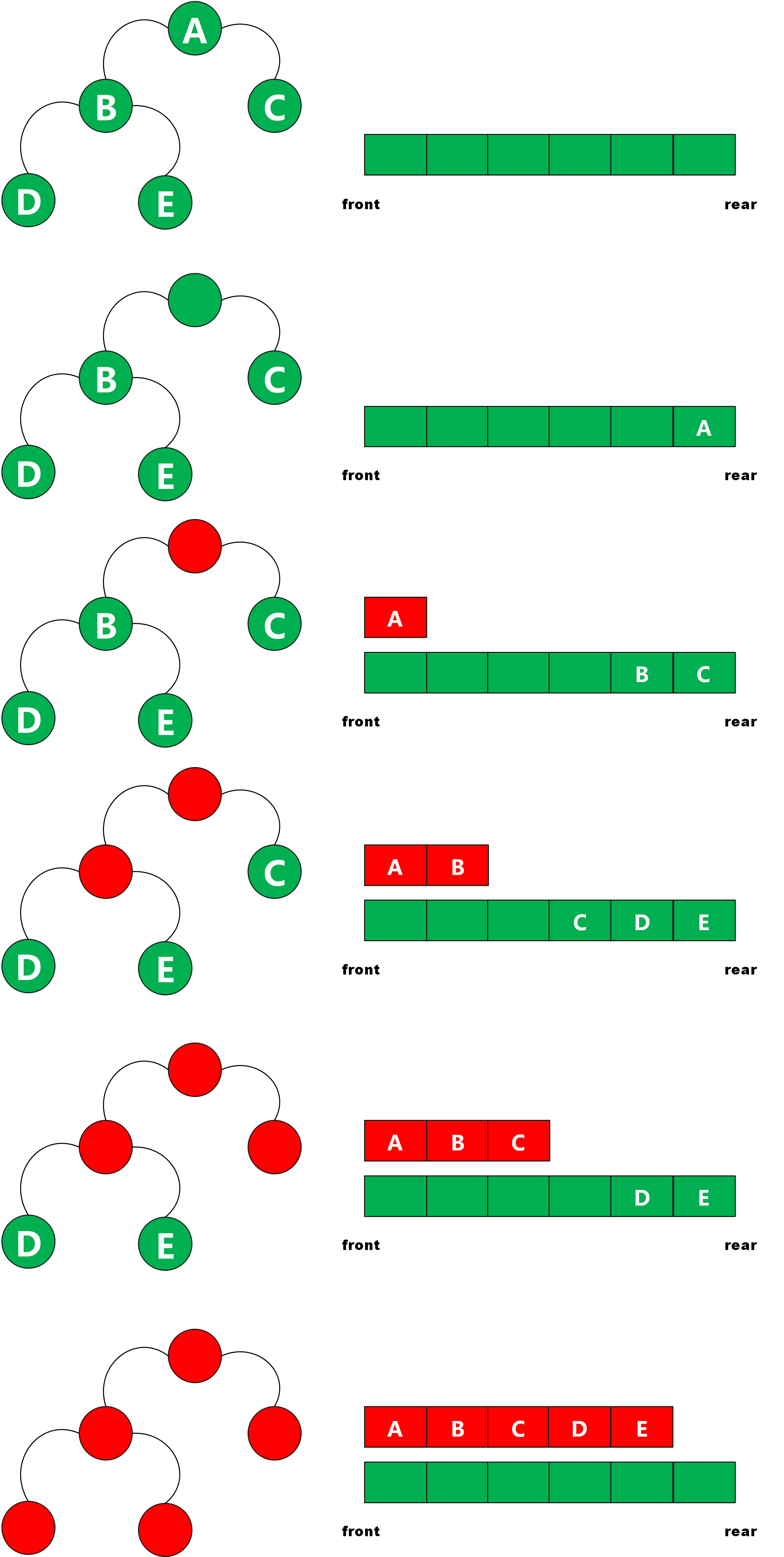
代码如下

void LevelOrder(BTNode* root)
{
	LinkQueue Q;
	InitQueue(Q);
	BTNode* p;//辅助结点
	EnQueue(Q,root);//先将根节点入队列
	while(isEmpty(Q))
	{
		DeQueue(Q,p);//出队列，p拿到结点
		visit(p);
		if(p->lchild!=NULL)
			EnQueue(Q,p->lchild);
		if(p->rchild!=NULL)
			EnQueue(Q,p->rchild);
	}
}

四：二叉树实现

package myBinaryTree;

import sun.reflect.generics.tree.Tree;

import java.time.temporal.Temporal;
import java.util.*;

public class MyBinaryTree {
    static class TreeNode {
        public char val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(char val) {
            this.val = val;
        }
    }

    //根节点
    public TreeNode root;

    //根据字符串序列创建二叉树（字符串序列表示某二叉树的先序遍历序列，例如ABC##DE#G##F###,其中
    //#表示空格，代表空树）
    public TreeNode createTree(String str){
        TreeNode root = null;
        if(str.charAt(i) != '#'){
            root = new TreeNode(str.charAt(i));
            i++;
            root.left = createTree(str);
            root.right = createTree(str);
        }else{
            i++;
        }
        return root;
    }

    //前序遍历-递归实现
    public void preOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        System.out.println(root.val + "；");
        preOrder(root.left);
        preOrder(root.right);
    }

    //前序遍历-非递归实现
    public void preOrderNoRecursive(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();//临时栈
        TreeNode cur = root;
        //遇到结点就访问然后入栈，并转向左节点
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                System.out.println(root.val + "：");
                stack.push(cur);
                cur = cur.left;
            }
            //循环停止时，走到了最左面的结点
            TreeNode tmp = stack.peek();
            stack.pop();
            //如果它没有右节点，那么就继续出下一个结点
            //如果它有右节点，那么右节点进入循环，然后入栈再重复
            cur = tmp.right;
        }
    }

    //中序遍历
    public void inOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        preOrder(root.left);
        System.out.println(root.val + "；");
        preOrder(root.right);
    }

    //中序遍历-非递归实现
    public void inOrderNoRecursive(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode tmp = stack.peek();
            stack.pop();
            System.out.println(tmp.val + "：");

            cur = tmp.right;
        }
    }

    //后序遍历
    public void postOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        preOrder(root.left);
        preOrder(root.right);
        System.out.println(root.val + "；");
    }

    //后序遍历-非递归实现
    //将前序遍历改为“根右左”，然后再反转结果，就是后序遍历
    public void postOrderNoRecursive(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                System.out.println(root.val + "：");
                stack.push(cur);
                cur = cur.right;
            }
            TreeNode tmp = stack.peek();
            stack.pop();
            cur = tmp.left;

            // Collections.reverse(ret);

        }
    }

    //获取树中结点的个数
    public int treeSize(TreeNode root) {
        if(root == null) return 0;
        return treeSize(root.left) + treeSize(root.right) + 1;
    }

    //获取树中叶子结点个数
    public int treeLeafNodeSize(TreeNode root){
        if(root == null) return 0;
        if(root.left == null && root.right == null) return 1;
        return treeLeafNodeSize(root.left) + treeLeafNodeSize(root.right);
    }

    //求第k层结点个数
    public int theNumOfk(TreeNode root, int k){
        if(root == null) return 0;
        if(k == 1) return 1;
        return theNumOfk(root.left, k-1) + theNumOfk(root.right, k-1);
    }

    //获取二叉树高度
    public int treeHeight(TreeNode root){
        if(root == null) return 0;
        if(root.left == null && root.right == null) return 1;
        int leftHeight = treeHeight(root.left);
        int rightHeight = treeHeight(root.right);
        return leftHeight > rightHeight ? leftHeight + 1 :rightHeight + 1;
     }

     //判断某个元素是否存在
    public TreeNode find(TreeNode root, char val) {
        if (root == null) return null;
        if (root.val == val) return root;

        TreeNode find_left = find(root.left, val);
        if (find_left != null) return find_left;
        TreeNode find_right = find(root.right ,val);
        if(find_right != null) return find_right;
        return null;
    }

    //层次遍历
    public void levelTraversal(TreeNode root){
        Queue<TreeNode> queue = new LinkedList<>(); //借助队列实现
        TreeNode temp;
        queue.offer(root);
        while(!queue.isEmpty()){
            temp = queue.poll();
            System.out.println(temp.val + ":");
            if(temp.left != null){
                queue.offer(temp.left);
            }
            if(temp.left != null){
                queue.offer(temp.right);
            }
        }
    }
}

目录CONTENT

第十四章第四节：Java集合框架之二叉树