一:栈基本概念
(1)栈的定义
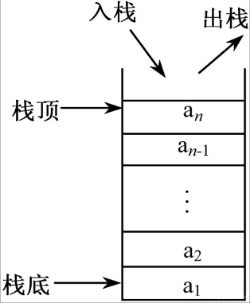
栈(stack):是一种将插入和删除操作限制在一端进行的线性表。其中允许插入和删除的一端称之为栈顶(top),另一端则称之为栈底(bottom)。不含任何数据元素的栈称之为空栈。栈中元素遵循后进先出原则
-
类似于弹夹中的子弹,先压进去的子弹是最后出来的

-
一些软件(例如Word,Photoshop)其撤销操作本质也是栈结构
(2)压栈和出栈
压栈:是栈的插入操作,也叫做进栈、入栈
出栈:是栈的删除操作,也叫做弹栈
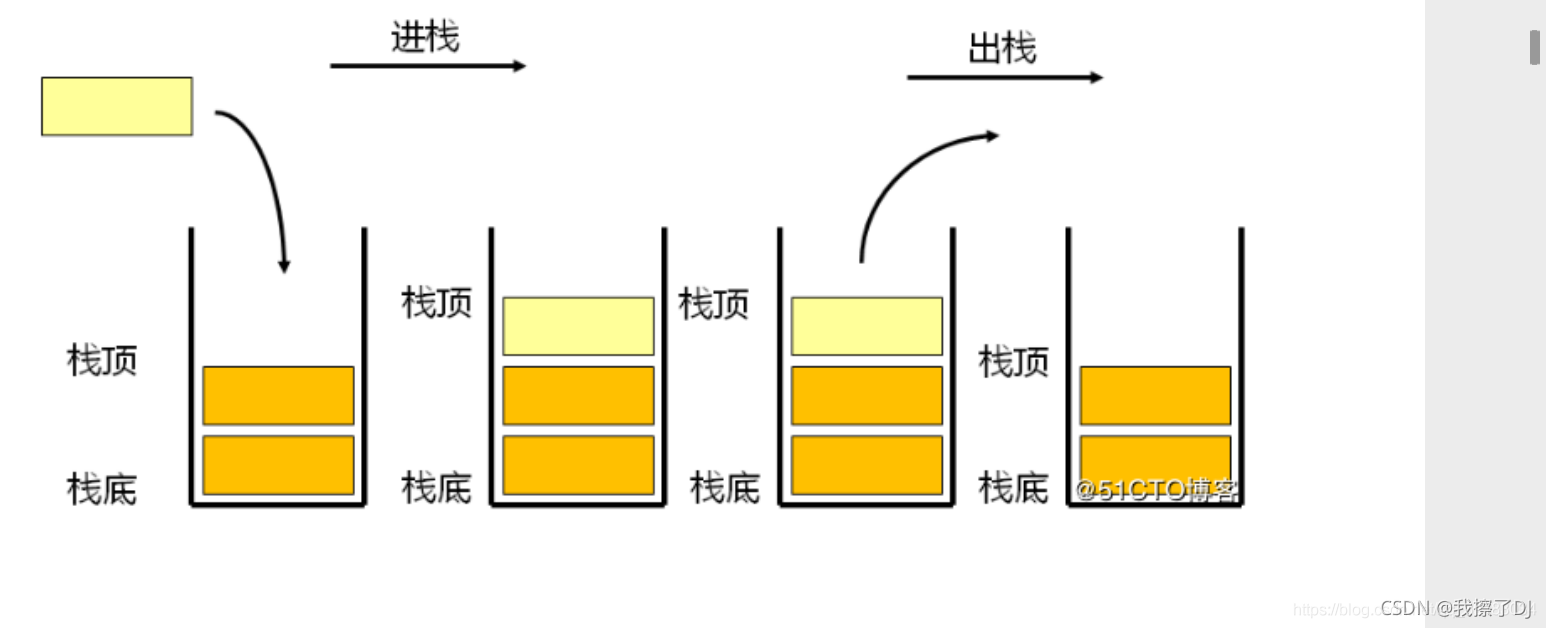
如下
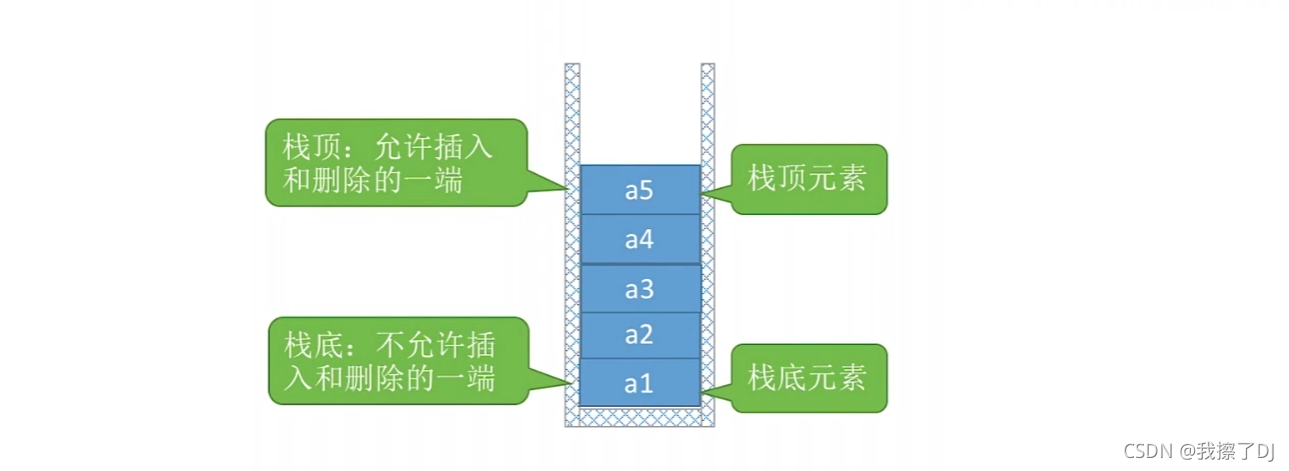
- 进栈顺序:a_{1}->a_{2}->a_{3}->a_{4}->a_{5}
- 出栈顺序:a_{5}->a_{4}->a_{3}->a_{2}->a_{1}
(3)进栈出栈变化形式
值得注意的是,栈对线性表的插入和删除是在位置上进行了限制,但是并没有对进出时机进行限制。也就说,刚进去的元素也可以立即出栈,只要保证位置是栈顶即可
比如现在有3个元素1、2、3依次进栈,会有哪些出栈次序呢?
- 第一种:1、2、3进,然后再3、2、1。出栈次序为321
- 第二种:1进、1出;2进、2出;3进、3出。出栈次序为123
- 第三种:1进、2进、2出、1出、3进、3出。出栈次序为213
- 第四种:1进、1出、2进、3进、3出、2出。出栈次序为132
- 第五种:1进、2进、2出、3进、3出、1出。出栈次序为231
列举完毕共有5种情况。除此之外,像312这种情况是绝对不可能出现的。因为3先出栈,就意味着3曾经进栈,既然3都进栈了,那么也就意味着1和2已经进栈了,此时2一定是在1的上面,出栈只能是321
其实,n个不同元素进栈,出栈元素不同排列的个数可由卡特兰(Catalan)数确定:
N=\frac{1}{n+1}C^{n}_{2n}
- 比如上面的3个元素就有\frac{1}{3+1}C_{6}^{3}=\frac{1}{4}×\frac{6×5×4}{3×2×1}=5种
- 卡特兰数证明有兴趣可以移步点击跳转
(4)栈的操作
一个栈的基本操作如下
InitList(&L):初始化表DestoryList(&L):销毁操作ListInsert(&L,i,e):插入操作ListDelete(&L,i,&e):删除操作LocateElem(L,e):按值查找GetElem(L,i):按位查找
其它常用操作
Length(L):求表长PrintList(L):输出操作Empty(L):判空操作
二:Stack使用
Stack:数据结构中的栈对应于Java集合框架中的Stack。从下图中可以看到,Stack继承了Vector,而Vector和ArrayList类似,都是动态顺序表,不过Vector是线程安全的
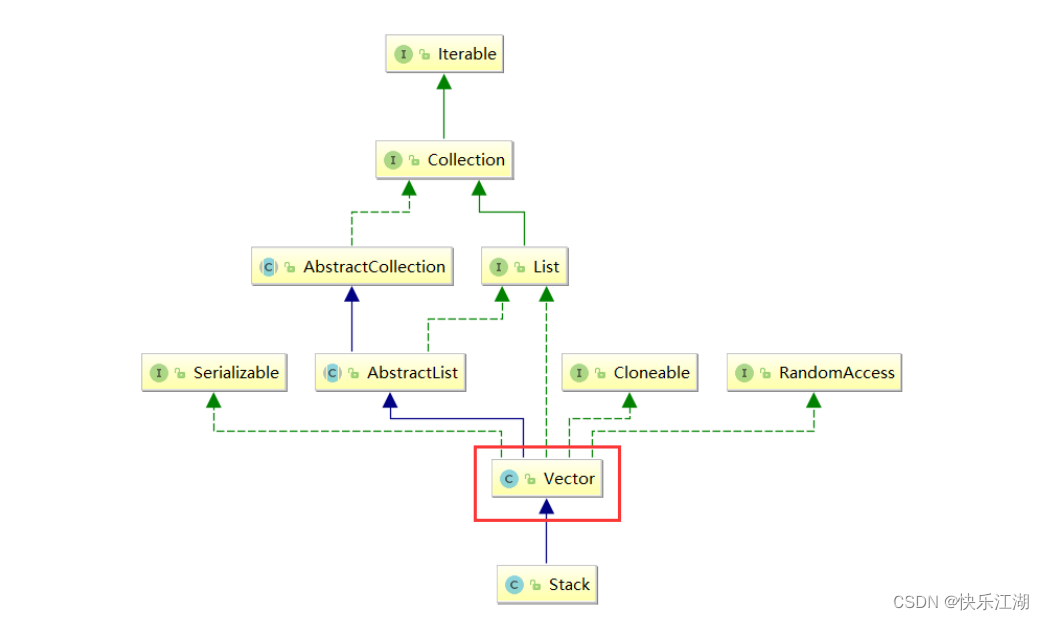
涉及方法如下
E push(E, e):将e入栈,并返回eE pop():将栈顶元素出栈并返回E peek():获取栈顶元素int size():返回栈中有效元素的个数boolean empty():检测栈是否为空
下面是一个例子
import java.util.Stack;
public class TestDemo {
public static void main(String[] args) {
Stack<Integer> s = new Stack<>();
s.push(12);
s.push(34);
s.push(56);
s.push(78);
s.push(90);
System.out.println("获取栈中有效元素个数:" + s.size());
System.out.println("获取栈顶元素:" + s.peek());
s.pop();
s.pop();
System.out.println("出栈两个元素并返回此时栈顶元素:" + s.peek());
System.out.println("判断栈是否为空:" + s.empty());
}
}

三:栈的模拟实现
- 栈的实现可以分为顺序栈和链栈两种,但链式结构并不常用,所用这里介绍顺序栈的实现
- 顺序栈底层其实是一个数组
(1)顺序栈
A:顺序栈的定义
顺序栈:顺序栈使用数组来实现。其中下标为0的一端作为栈底,将数组尾部作为栈顶,以进行插入和删除
由于尾部元素作为栈顶,也即最后一个元素是栈顶元素,所以需要使用一个 变量top 进行标识,top之外元素将不属于栈的定义范围,通常把top=-1定义为空栈
- 这有点像游标卡尺的游标,游标(
top)可以随意变大或变小,但是不能超出尺子的范围

因此顺序栈结构定义如下
#define MaxSize 10
typedef struct SqStack
{
DataType arr[MaxSize];
int top;//栈顶指针
}SqStack;
假定MaxSize=5,顺序栈常见的情况如下
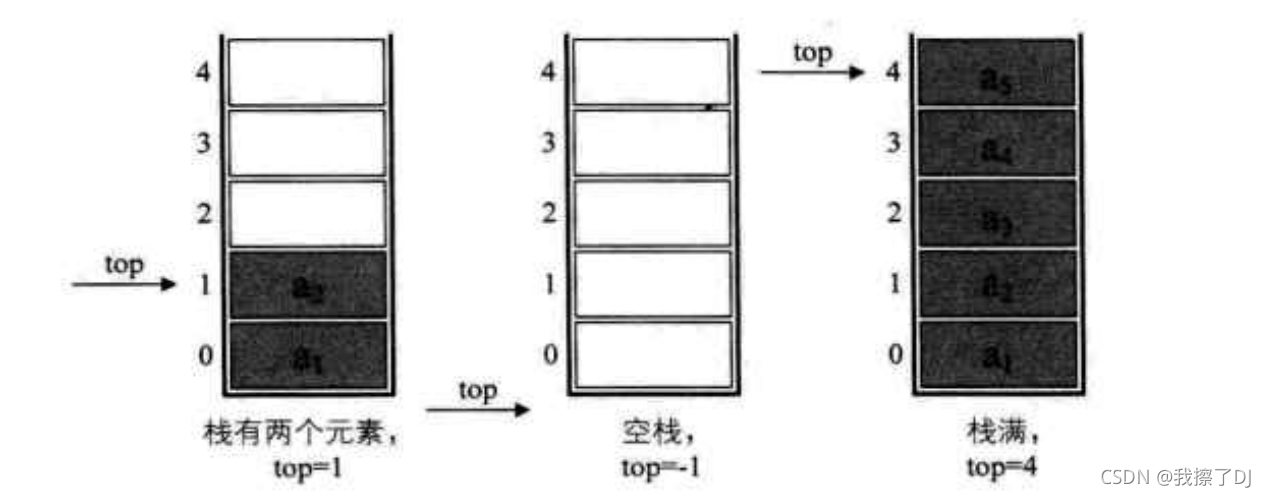
- 其中栈空的充要条件为
top==-1
B:进栈
进栈:进栈时,先栈顶指针+1,后进行元素赋值(若top初值为0逻辑恰好相反)
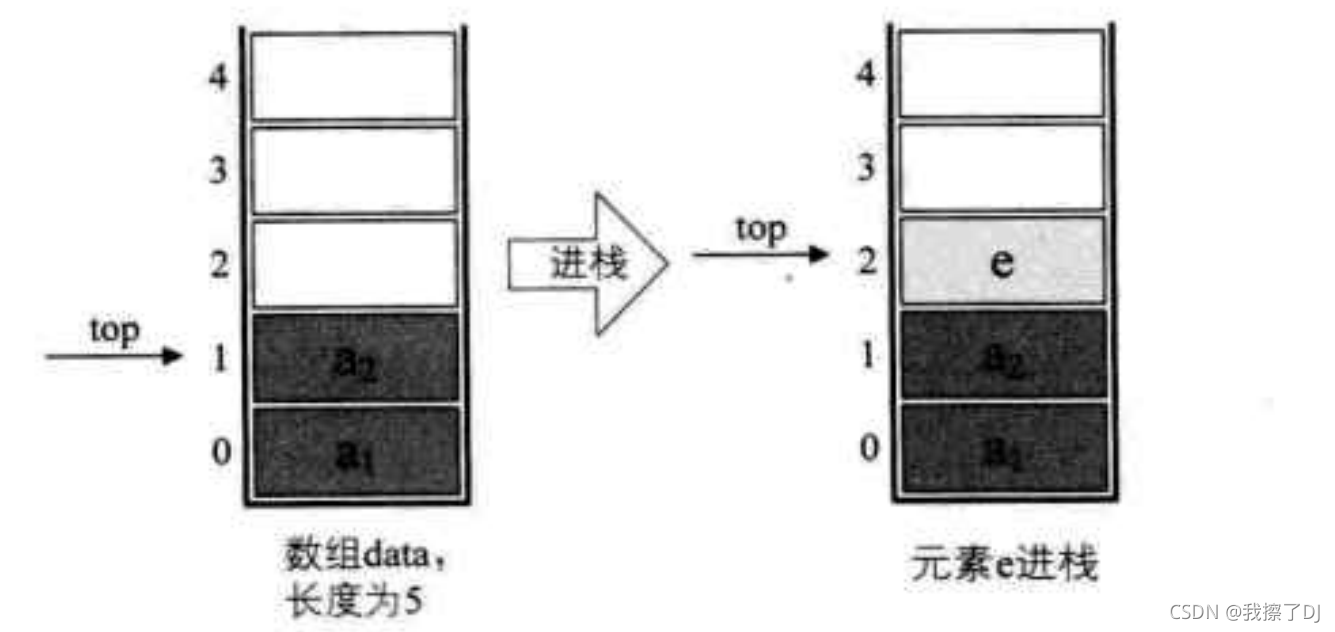
代码如下,注意栈满判断
bool Push(SqStack& S,Datatype e)
{
if(S.top==MaxSize-1)
return false;//栈满
S.top+=1;
S.data[S.top]=e;
return true;
}
C:出栈
出栈:出栈时,先保存元素,后栈顶指针-1(若top初值为0逻辑恰好相反)
- 注意这种删除只是逻辑上的删除,其元素仍然会留在那片区域里。因为我们研究的是栈,只研究的是
0~top这个范围内的情况
代码如下,注意栈空判断
bool Pop(SqStack& S,DataType& e)
{
if(S.top==-1)
return false;//栈空
e=S.data[S.top];
S.top-=1;
return true;
}
D:读取栈顶元素
代码如下
bool GetTop(SqStack& S,DataType& e)
{
if(S.top==-1)
return false;//栈空
e=S.data[S.top];
return true;
}
(2)代码
package myStack;
import java.util.Arrays;
public class MyStack {
public int[] elem;
public int usedSize;//当前栈中有效元素个数,也即top指针
public static final int DEFAULT_CAPACITY = 10;//默认容量
public MyStack(){
elem = new int[DEFAULT_CAPACITY];
}
//压栈
public void push(int val){
//如果栈满则扩容
if(isFull()){
elem = Arrays.copyOf(elem, 2*elem.length);
}
//放置元素,并移动指针
elem[usedSize] = val;
usedSize++;
}
//判满
public boolean isFull(){
if(elem.length == usedSize){
return true;
}
return false;
}
//出栈
public int pop(){
//判空
if(isEmpty()){
throw new StackEmptyException("栈空!无法删除");
}
int retVal = elem[usedSize-1];;
usedSize--;
return retVal;
}
//判空
public boolean isEmpty(){
if(usedSize == 0){
return true;
}
return false;
}
//查看栈顶元素
public int peek(){
//判空
if(isEmpty()){
throw new StackEmptyException("栈空!无法删除");
}
return elem[usedSize-1];
}
//返回栈顶有效元素个数
public int size(){
return usedSize;
}
}
四:栈的一些应用
栈主要在以下场景中会涉及到


评论区